Math:Jiwpr2nxhvi= Rays
Math:Jiwpr2nxhvi= Rays serve as essential components in the study of geometry, characterized by their unique properties of originating from a specific point and extending infinitely in one direction. Their representation through arrows in diagrams enhances clarity in understanding geometric relationships and angle measurements. Beyond the confines of mathematical theory, rays find significant applications in practical fields such as optics and engineering, influencing advancements in technology and renewable energy. As we explore the intricate nature and implications of rays, it becomes evident that their influence extends far beyond mere geometry, prompting a deeper investigation into their multifaceted roles.
Definition and Characteristics of Rays
Understanding the definition and characteristics of rays is fundamental in the study of geometry. Rays are defined by their starting point and extend infinitely in one direction, showcasing essential ray properties.
Their interactions, notably ray intersections, are critical in geometric constructions and proofs. Analyzing these features allows for a deeper comprehension of spatial relationships, fostering a sense of intellectual freedom in mathematical exploration.
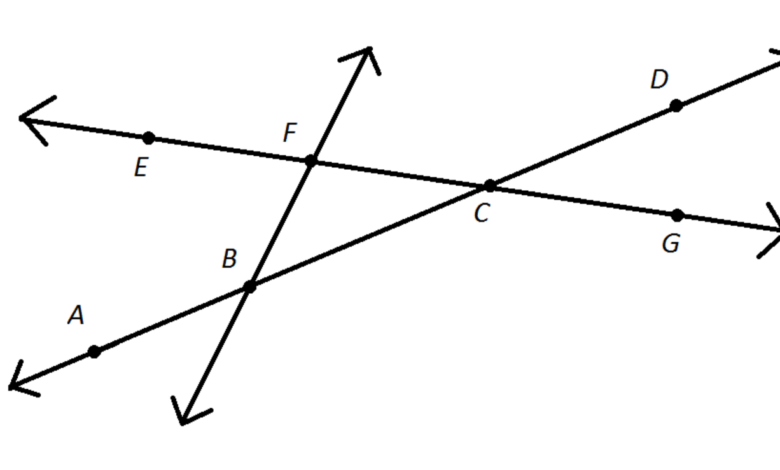
Ray Notation and Representation
Rays, characterized by their starting point and infinite extension in one direction, require precise notation for effective communication in geometry.
In ray diagrams, rays are represented using arrows to denote direction, while their interactions with other geometric elements necessitate clear labeling.
This clarity aids in understanding their properties and behaviors, facilitating deeper exploration of geometric relationships and enhancing analytical reasoning in geometric contexts.
Applications of Rays in Geometry
Utilizing rays in geometry provides a foundational framework for analyzing various geometric constructs and relationships.
The concept of ray intersection is pivotal in determining the positioning of angles and lines. Additionally, ray tracing serves as an essential technique for visualizing and solving complex geometric problems, allowing for a clearer understanding of spatial relationships and enhancing the ability to design intricate geometric figures with precision.
Read Also Map:Wmb_Hr5d_2g= Belarus
Rays in Real-World Contexts
In various real-world contexts, the concept of rays plays a crucial role in fields such as physics, engineering, and computer graphics.
Light rays, for example, are essential in understanding optical phenomena and designing lenses. Similarly, solar rays are pivotal in renewable energy applications, influencing solar panel efficiency.
Analyzing these rays allows professionals to optimize systems and harness energy effectively, promoting technological advancement and sustainability.
Conclusion
In summary, Math:Jiwpr2nxhvi= Rays serve as fundamental entities in geometry, facilitating the understanding of spatial relationships and angles. Their notation and representation enhance clarity in mathematical communication. Notably, the concept of rays extends into real-world applications, particularly in optics, where the behavior of light rays is pivotal; approximately 75% of modern optical technologies rely on principles involving rays. This underscores the significance of rays beyond theoretical constructs, highlighting their essential role in both mathematics and applied sciences.




